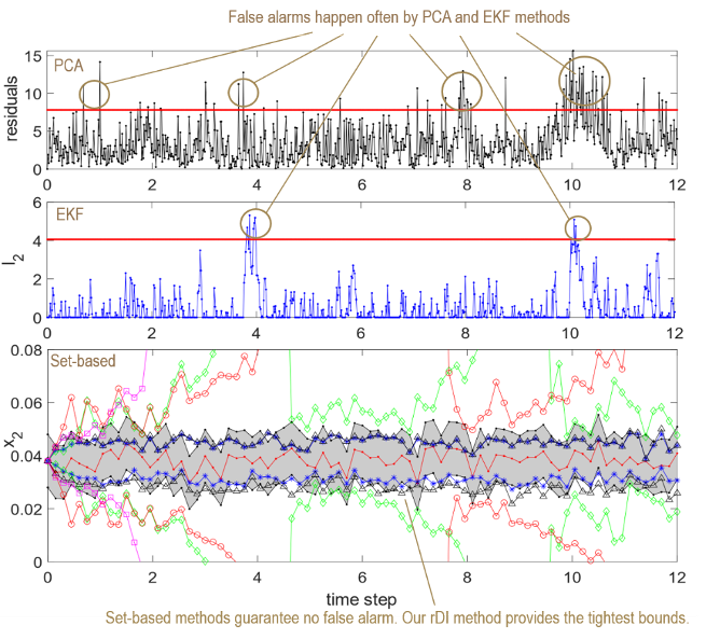
Uncertainty Propagation and Fault Detection
In applications such as chemical processing, wind energy, and industrial robotics, increases in complexity and automation have made component malfunctions and other abnormal events a threat to safety and reliability. FDD algorithms have become an essential feature of modern control systems, leading to significant decreases in downtime, maintenance costs, and catastrophic failures. In this project, we develop a fast and accurate set-based state estimation algorithm for detecting deviations from a given fault-free model subject to bounded uncertainties, and an algorithm for designing efficient and highly accurate set-membership tests for diagnosing faults from a given library of fault models. The capabilities of these algorithms will be demonstrated in real systems.
Student: Bowen Mu
Recent publication: Mu, B., Yang, X., and Scott, J. K. Computers & Chemical Engineering, 166, 107975 (2022)
Decomposition Strategies for Large-Scale Global Optimization
Stochastic programming is a powerful optimization framework for modeling decision-making under uncertainty and is highly advantageous, e.g., in planning and process control, where much information is not known with certainty when decisions are made. However, stochastic programming models often involve a very large number of variables and constraints. For nonconvex models, this makes it prohibitively expensive to find global solutions, at least by direct application of standard global optimization algorithms. As a result, there is significant interest in decomposition-based techniques that can transform a stochastic programming problem into a sequence of smaller subproblems that can be solved more efficiently and largely in parallel, while still providing a rigorous guarantee of global optimality. We are interested in better understanding existing decomposition methods and proposing new decomposition frameworks which avoid the cluster problem by analyzing the convergence rates of these methods and its connection with the accuracy of lower bounds in spatial branch and bound algorithm.
Students: Pengfei Cheng, Dillard Robertson
Modeling and Simulation of Intensified Chemical Processes
Process intensification (PI) is continuously evolving as a viable solution for sustainable growth by providing a means for improving energy efficiency, productivity, and reducing global emission footprints of important chemical processes. However, one of the remaining barriers for realizing PI is lacking reliable modeling tools for newly emerging classes of intensified chemical processes. We are currently interested in modeling opportunities in intensified separation processes, including membrane and pressure swing adsorption (PSA) processes. For membrane processes, we are creating efficient and reliable numerical methods for simulating local fluxes of complex mixture permeation. Also, we are extending these models into the overall global membrane module for more realistic process design and performance evaluation. For PSA processes, we are developing rules for automatically making near-optimal operational and design decisions. Furthermore, we are developing numerical methods for incorporating recent advancements in adsorption isotherm and rate models into PSA process simulators.
Students: Taehun Kim, Dylan Weber
Recent publication: Mathias, R., Weber, D. J., Thompson, K. A., Marshall, B. D., Finn, M. G., Scott, J. K., & Lively, R. P. Journal of Membrane Science, 640, 119767.
Modified Rules for Computing Convex and Concave Relaxations to Bound Real Functions for Global Optimization
The ability to produce convex and concave relaxations of real functions, or the lower and upper bounds of real functions in convex and concave geometries respectively, is useful in a variety of optimization problem-solving contexts, ranging from reduced-space global optimization to global dynamic optimization. These relaxations are computed by recursively propagating a set of rules to bound, as input, the results of elementary operations such as the composition of a function within a univariate (e.g., square) outer function, all of which make up the larger function we want to bound ultimately. Ideally, we should be capable of also computing relaxations of desired convexity and concavity for a function whose input relaxations are crossed, in which case due to infeasibility in some constraints on some parts of a domain, the input's convex relaxation is above, rather than below, the corresponding concave relaxation in those infeasible parts of the domain. By bounding the objective function over only the potentially feasible parts of a domain, the resulting bounds can be much tighter than otherwise, as per interval arithmetic. However, crossed input relaxations are not propagated properly to output using the existing rules for computing relaxations, since either the convex relaxation of the output function can be nonconvex or its concave relaxation can be nonconcave. To this end, we are reformulating the existing rules for computing the relaxations of elementary operations, so that the relaxations remain convex and concave even if any input relaxations cross. This is the first step towards balancing the need for tight bounding by relaxations with the need to guarantee their desired convexity, for application to global optimization.
Student: Jason Ye
FLExible Carbon Capture and Storage (FLECCS)
The nullification of the anthropogenic carbon dioxide (CO2) emissions is the most significant action to stop global warming, also the reduction of the existing CO2 from the environment is a key recourse to adjust the global temperature to preindustrial levels. For these reasons the Direct Air Capture (DAC) is a technology that offers a possible pathway to achieve these objectives.
Moreover, it is projected that the future of the electricity production in the United States will consists of a portfolio of high penetration of renewables, thus the existing fuel-to-electricity generators need to be adjusted to consider both the high variability of the electricity cost and the zero-emission policy. Therefore, as part of the FLECCS program, we intent to model a retrofit the existing standard for Natural Gas Combined Cycle (NGCC) plant with a Post Combustion Capture (PCC) process and DAC such that the operational degrees of freedom, e.g., gas turbine load factor, DAC sorbent allocation, etc. are found by solving a mathematical optimization program for an arbitrary time horizon under variable levelized costs of electricity. Preliminary results show that in order to maximize the gross profit of the plant, the DAC must be used more aggressively whenever the cost of power is low, in this way the plant generates negative emission levels and hedges against the variability of the costs.
Students: Pengfei Cheng, David Thierry
Optimization of the AC Optimal Power Flow Problem
The Optimal Power Flow (OPF) problem refers to a class of optimization formulations where the generation levels of all generators on a power grid are determined to optimality. Variants of the OPF can also be used in many other power grid related formulation. Currently there is no method for solving the OPF which is both fast enough for common use, and accurate enough to give results which are actually optimal. The AC Optimal Power Flow (ACOPF) problem is an accurate OPF problem, but solving this problem globally is currently too slow for use in many situations. We are interested in finding techniques to solve the ACOPF problem fast enough for use by power grid operators. One useful category of techniques is Optimality Based Bounds Tightening (OBBT), which operate by reducing the search space for an optimization problem. For many power grids, OBBT techniques have been observed reduce the search space of the ACOPF problem down to the optimal solution. We are creating a technique that combines an optimized OBBT technique for speed and Branch and Bound to reliably generate a solution if OBBT fails to find the optimal solution.
Student: Dillard Robertson